| もどる | next(スカラー場の微分) |
物理学では場(Field)の概念がよく用いられる。例えば、電場や磁場はよく用いられている場の概念の例である。ここでは、場の定義をしてみたいと思う。
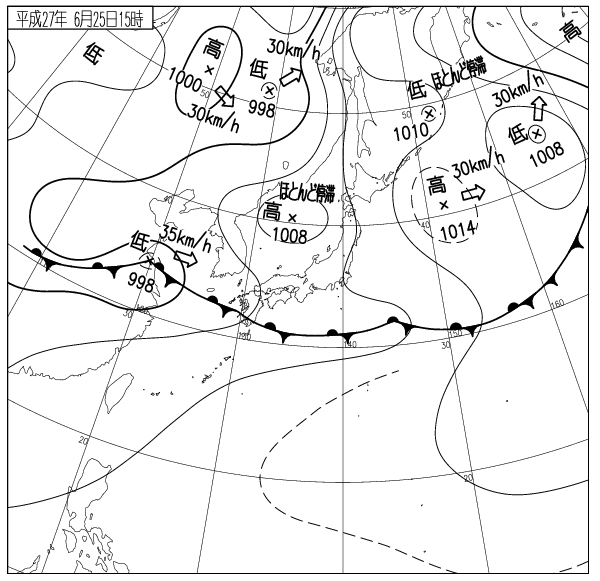
ある場において、位置と時間を指定すれば、場の物理量の値が一意的に決定される。場を考えることの利点は、物理量を空間の上にマッピングできるという点にある。例えば、気圧(圧力)という物理量は、地球上のある点、ある時刻で一意的な値を取ることができ、気圧の場を考えることができる。これをマッピングしたものの例として挙げられるのが、天気図である(Fig.1)。

天気図には、気圧のほかにも、気温(温度)、風向風速などの物理量も記されていて、これらの物理量も場としての表現が可能である。特に、場の物理量がスカラーとして与えられるような場を、スカラー場(Scalar field)といい、場の物理量がベクトルで与えられる場をベクトル場(Vector field)と呼ぶ。気圧の場(圧力場)や気温の場(温度場)はスカラー場、風ベクトルの場(速度場)はベクトル場である。
このスカラー場、ベクトル場を数学的に定義してみよう。スカラー場はある時刻$t$、ある空間の一点$(x_1,x_2,\cdots,x_n)$からスカラー量$\phi_0$を一意的に定めるので、 \[\phi:\mathbb{R}^{n+1}\ni(x_1,x_2,\cdots,x_n,t)\mapsto\phi_0\in\mathbb{R}\] なる写像$\phi$がスカラー場の正体である。時間を固定できる場合は、変数を一つ減らすことができ、 \[\phi:\mathbb{R}^n\ni(x_1,x_2,\cdots,x_n)\mapsto\phi_0\in\mathbb{R}\] なる写像$\phi$でスカラー場が定義できる。他の文献では時間を固定した定義の方が多く見受けられる。一方、ベクトル場は、スカラー場と同様にして、 \[\psi:\mathbb{R}^{n+1}\ni(x_1,\cdots,x_n,t)\mapsto\mathbb{R}^n\in(\psi_1,\cdots\psi_n)\] なる写像$\psi$で定義できる。ベクトル場はベクトルへの写像なので、写像と関数の類似性の立場からベクトル値関数(Vector-valued function)とも呼ばれる。ベクトル場の場合も、時間を固定する場合の定義が多く見受けられ、 \[\psi:\mathbb{R}^n\ni(x_1,\cdots,x_n)\mapsto\mathbb{R}^n\in(\psi_1,\cdots\psi_n)\] なる写像$\psi$としてベクトル場を定義することができる。この定義は有用で、時間に陽に依存しないベクトル場は写像の値域が定義域である$\mathbb{R}^n$の部分集合とできるため、$\mathbb{R}^n$上の「変換」として扱うことができる。
場を具体的に表現することを考える。空間次元を3次元とすれば、スカラー場は時空変数$x,y,z,t$からあるスカラー量$\phi$を一意的に定めるので、 \[\phi=\phi(x,y,z,t)\] というふうに、4変数関数として表すことができる。逆に,4変数関数として表現できるものは3次元空間上のスカラー場となるので、例えば、 \[f_1(x,y,z,t)=\exp(\omega t-k_1x-k_2y-k_3z),\ f_2(x,y,z,t)=\sqrt{x^2+y^2+z^2-t^2}\] などもスカラー場である。むろん、スカラー場のもともとの定義は「スカラー量への写像」であるため、陽に多変数関数で表現しなくてもよい。たとえば、時間を固定したとき、線型関数で表現されるスカラー場は位置ベクトルへの内積で表現するのも有用である: \[f_3(x,y,z,t)=ax+by+cz=\begin{pmatrix}a&b&c\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}.\] 同様にして、発散$\mathrm{div}(\bullet)=\nabla\cdot\bullet=(\partial/\partial x, \partial/\partial y, \partial/\partial z)\cdot\bullet$($\cdot$は内積)のような位置ベクトルへ作用する演算子もスカラー場の一種とみなすことができる。
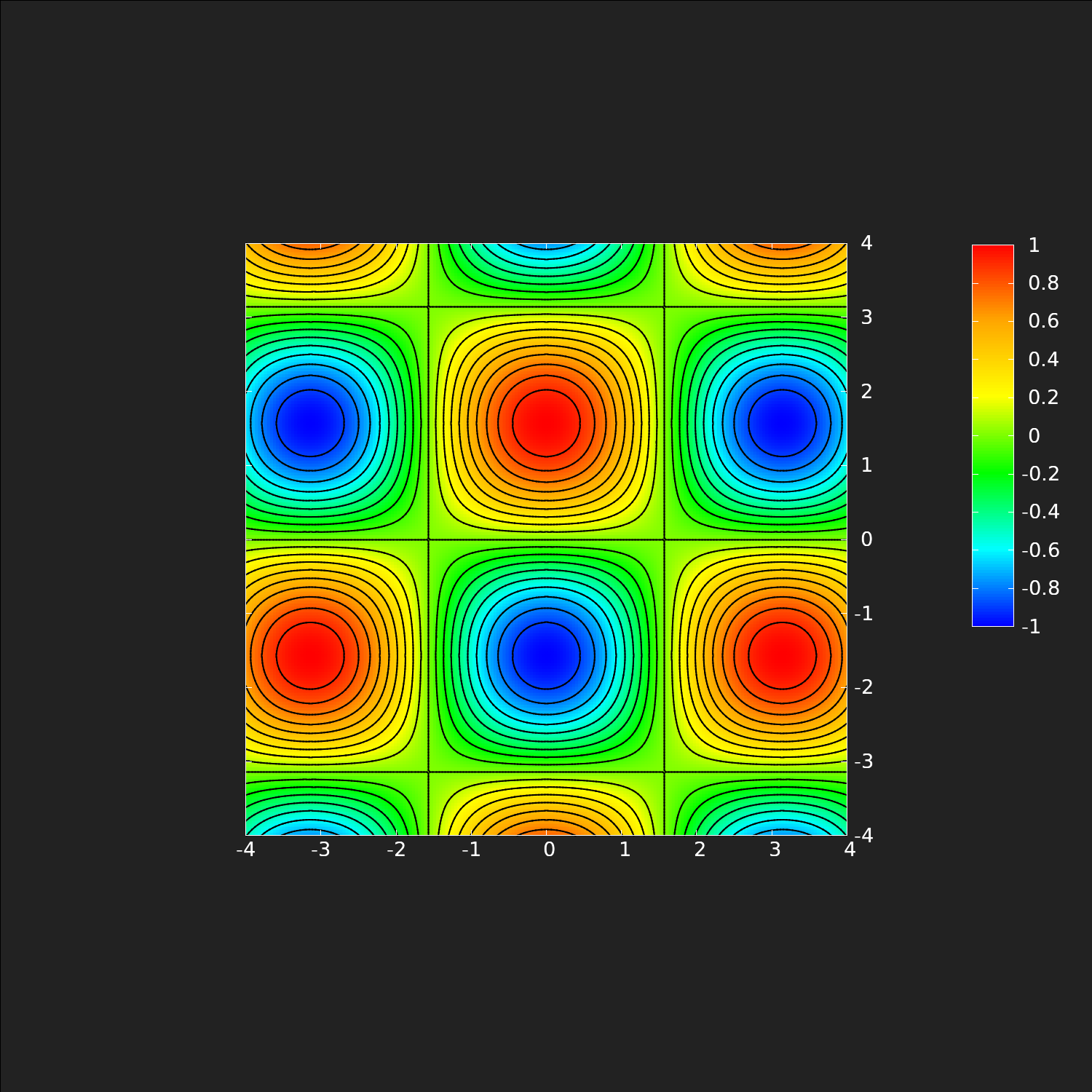
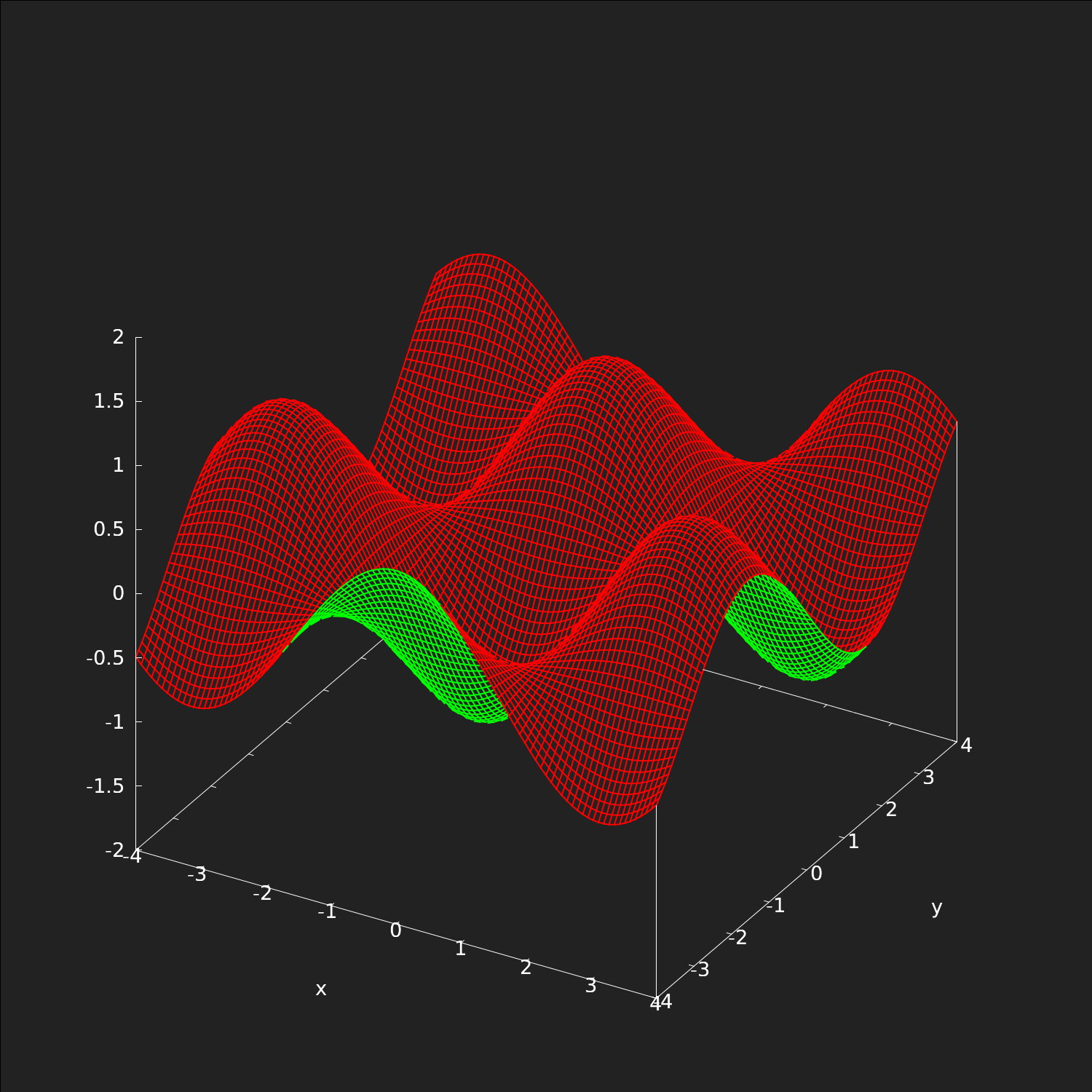
スカラー場を図示する方法としては、天気図の例で示したような等値線(等高線)図での表現が簡単だが、次元を一つ増やして、グラフとしても表現できる(Fig.2)。
一方、ベクトル場はベクトル値を返すため、各ベクトルの成分を並べて、 \[\vec{A}=\vec{A}(x,y,z,t)=(A_x(x,y,z,t),A_y(x,y,z,t),A_z(x,y,z,t))\] というふうに表記することができる。例えば、 \[\vec{A}_1(x,y,z,t)=(x\cos(\omega t),y\sin(\omega t),z),\vec{A}_2(x,y,z)=(y,-x,\exp(-zt))\] などはベクトル場である。また、ベクトル場も元々は単なる写像であるから、陽に関数を用いて表現しなくてもよい。例えば、時間に陽に依存しないベクトル場は$\mathbb{R}^n$上の変換としてとらえることができ、特に各成分が線型関数のときは位置ベクトルへの行列の積として表現することができる: \[ \vec{A}_3(x,y,z)=(ax+by+cz,dx+ey+fz,gx+hy+iz)= \begin{pmatrix} a&b&c\\ d&e&f\\ g&h&i \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix}. \] ほかにも、(偏)微分、たとえば、 \[\left(y^2\frac{\partial}{\partial x}+2x\frac{\partial}{\partial y}\right)\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}y^2\\2x\\0\end{pmatrix}\] や回転$\nabla\times \bullet$などの位置ベクトルへ作用する演算子によってもベクトル場を定義できる。このとき、演算子そのものをベクトル場と表現することがよくあるため、多変数関数の列挙によるベクトル場の定義に慣れている人は注意が必要である。多変数関数を列挙した形に直したければ、位置ベクトル$(x,y,z)$に演算子を作用させて計算すればよい。
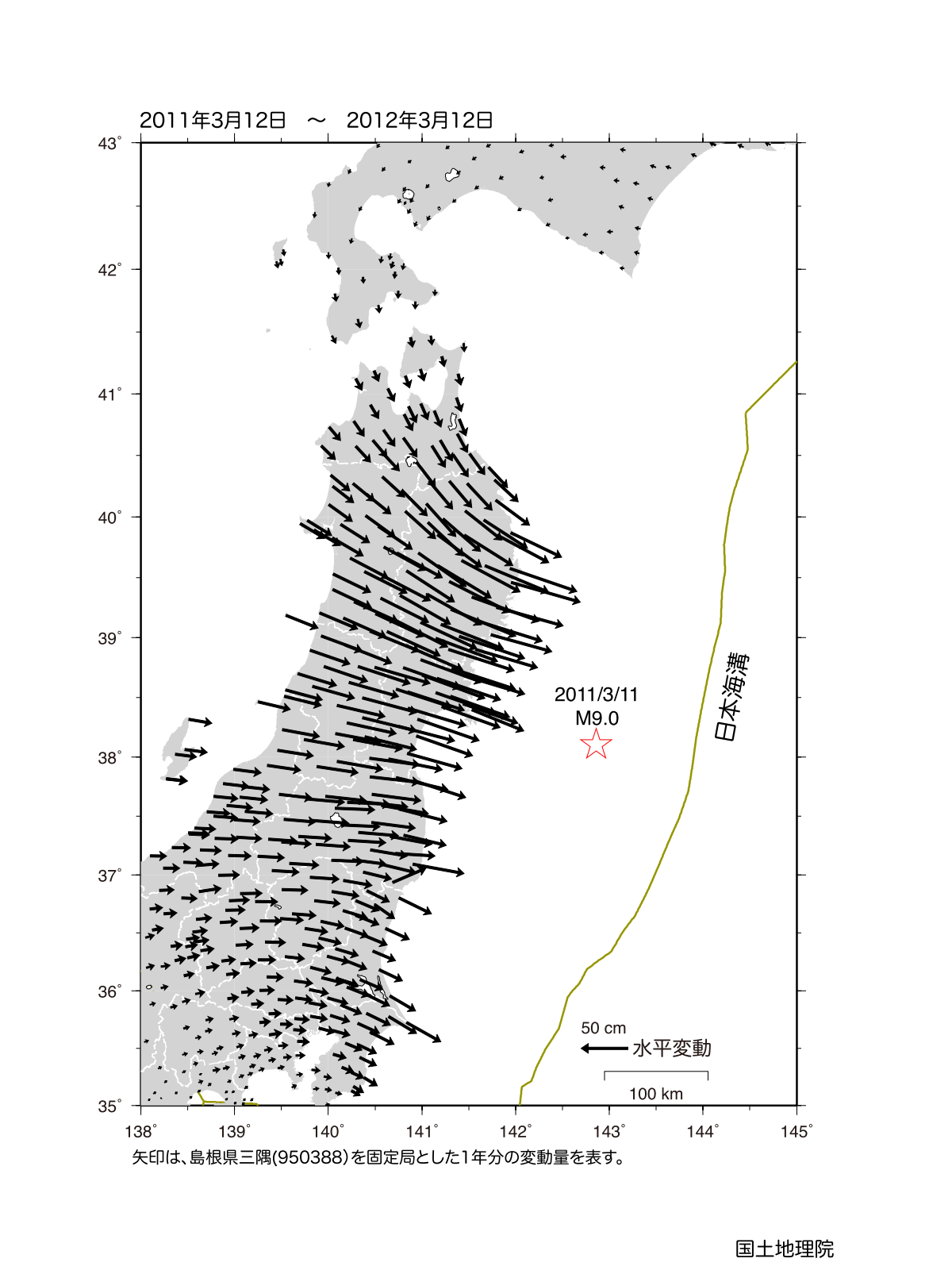
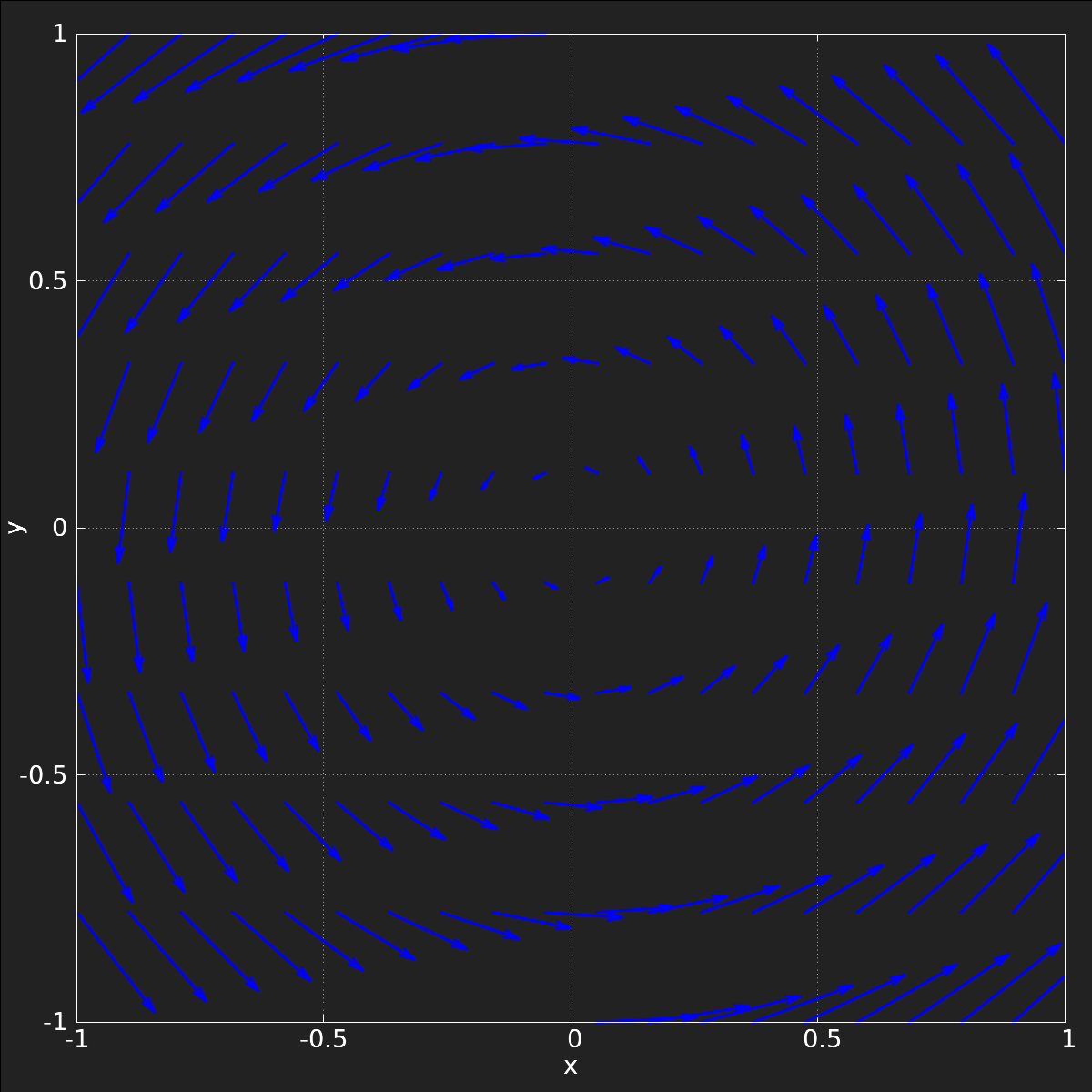
ベクトル場の図示は、それぞれの位置にベクトルをマッピングすることで行うことができる。日常場面では、地殻変動の表現や、天気図上の風向風速の表現などに見られる(Fig.3)。
| もどる | next(スカラー場の微分) |
Copyright (C) Matsuoka Ryo All Rights Reserved.
Last update: 2020/08/26