| もどる | next() |
ここでは、回転軸$\vec{d}$と回転角$\phi$による回転操作を表現するRodriguesの回転公式についてまとめる。
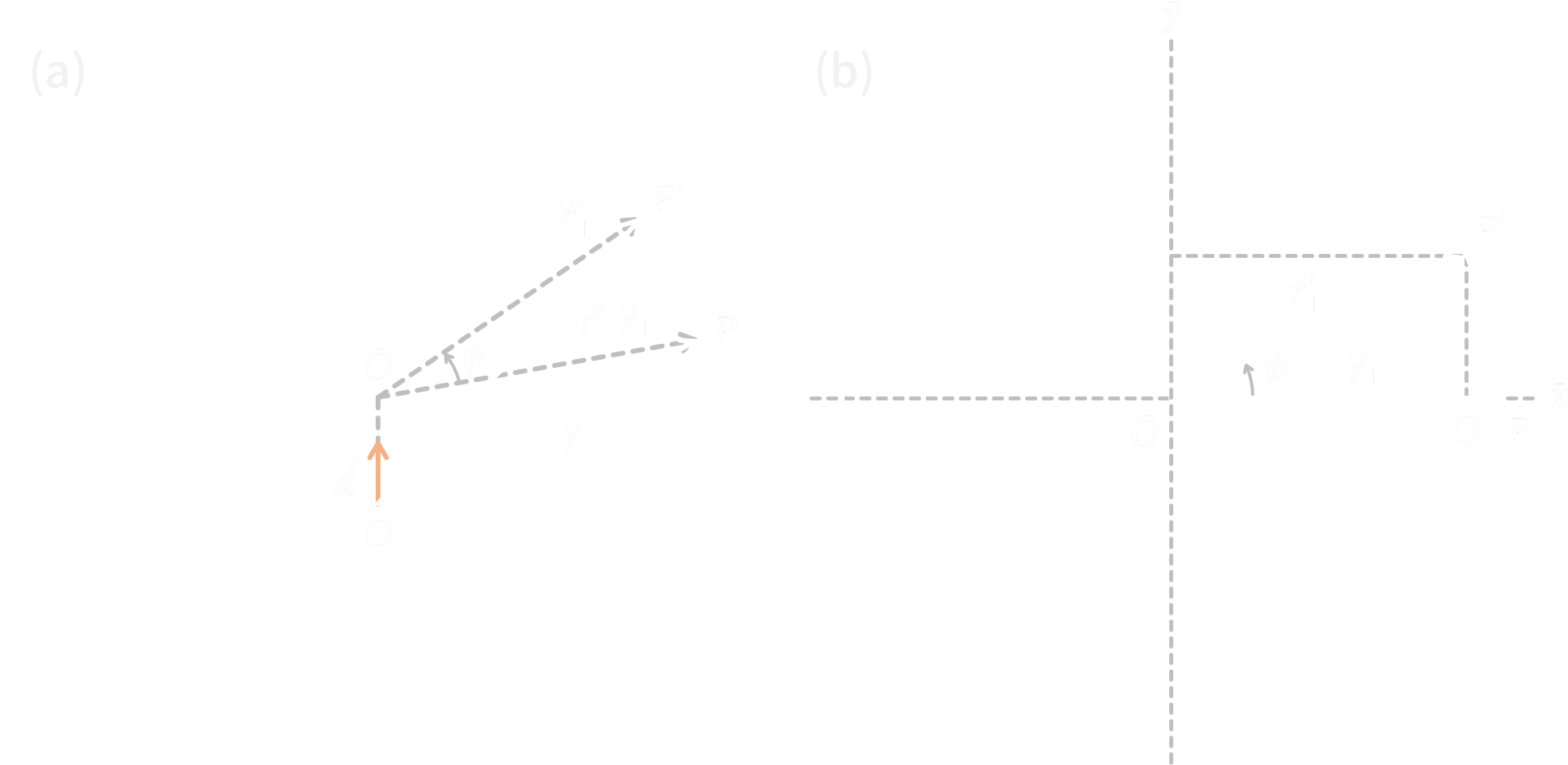
回転軸$\vec{d}$と回転角$\phi$による回転操作を考える。このとき、$\vec{d}$は単位ベクトルであるとし、角度は$\vec{d}$の方向を向いたときに反時計回りが正となるようにする。この回転操作によって、位置ベクトル$\vec{r}$が$\vec{r}'$に写されるとしよう (Fig. 1 (a))。さらに、$\vec{r}, \vec{r}'$の、$\vec{d}$と直交する面への射影を取ったものをそれぞれ、$\vec{r}_\perp, \vec{r}_\perp'$とする。この面内で原点$\bar{O}$を改めて取り、$\vec{r}_\perp$方向に$\bar{x}$軸を、そこから反時計回り垂直方向に$\bar{y}$軸を置くことにする (Fig. 1 (b))。

Fig. 1 を見れば、明らかに \[\vec{r}'=\vec{r}+\overrightarrow{PQ}+\overrightarrow{QP'}\tag{1}\] である。ここで、$\overrightarrow{PQ}, \overrightarrow{QP'}$はそれぞれ、$\bar{x}$軸、$\bar{y}$軸方向のベクトルであることに着目する。これらを適切に表現するためには、各軸方向の正規基底ベクトル$\vec{e}_\bar{x}, \vec{e}_\bar{y}$を調べればよい。
まず、$\vec{e}_\bar{y}$について考察してみよう。$\vec{e}_\bar{y}, \vec{d}, \vec{r}_\perp$は互いに直交しているため、 \[\vec{e}_\bar{y}=-\vec{d}\times\frac{\vec{r}_\perp}{|\vec{r}_\perp|}\tag{2}\] となる。ここで、$\vec{r}_\perp$は長さが1とは限らないので、正規化するために係数が掛かっていることに注意する。一方で、$\vec{r}$が$\vec{r}=\vec{r}_\parallel+\vec{r}_\perp$というふうに、$\vec{r}_\perp$と$\vec{d}$に平行なベクトル$\vec{r}_\parallel$に成分分解できることに着目すれば、 \begin{align*} \vec{d}\times\vec{r}&=\vec{d}\times(\vec{r}_\parallel+\vec{r}_\perp)\\ &=\vec{d}\times \vec{r}_\parallel+\vec{d}\times\vec{r}_\perp\\ &=\vec{d}\times\vec{r}_\perp. \end{align*} この式変形では、$\vec{d}$と$\vec{r}_\parallel$が平行であることから従う$\vec{d}\times\vec{r}_\parallel=\vec{0}$が用いられている。この結果から、(2)は \[\vec{e}_\bar{y}=-\frac{1}{|\vec{r}_\perp|}\vec{d}\times \vec{r}\tag{3}\] と書くことができる。次に$\vec{e}_\bar{x}$について考えてみると、これは$\vec{e}_\bar{x}, \vec{e}_\bar{y}, \vec{d}$が正規直交系をなしているという事実を使えばよい。すなわち、 \[\vec{e}_\bar{x}=\vec{d}\times\vec{e}_\bar{y}=-\frac{1}{|\vec{r}_\perp|}\vec{d}\times(\vec{d}\times\vec{r})\tag{4}\] とできる。
各軸方向の正規基底ベクトル(3), (4)の具体的な形が分かったので、これらを用いて$\overrightarrow{PQ}, \overrightarrow{QP'}$を表してみよう。Fig. 1 (b) を見れば、 \begin{align} &\overrightarrow{PQ}=-|\vec{r}_\perp|(1-\cos\phi)\vec{e}_\bar{x}=(1-\cos\phi)\vec{d}\times(\vec{d}\times\vec{r}),\tag{5}\\ &\overrightarrow{QP'}=|\vec{r}_\perp|\sin\phi\,\vec{e}_\bar{y}=-(\sin\phi)\,\vec{d}\times\vec{r}\tag{6} \end{align} と表されることがわかる.これらを(1)へ代入することで、 \[\vec{r}'=\vec{r}-(\sin\phi)\,\vec{d}\times\vec{r}+(1-\cos\phi)\,\vec{d}\times(\vec{d}\times\vec{r})\tag{7}\] を得る。
この回転操作の表現行列は簡単に求められる。外積の表現行列を用いればよい: \[\vec{a}\times\vec{x}= \begin{pmatrix} a_2x_3-a_3x_2\\ a_3x_1-a_1x_3\\ a_1x_2-a_2x_1 \end{pmatrix} = \begin{pmatrix} 0&-a_3&a_2\\ a_3&0&-a_1\\ -a_2&a_1&0 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \hat{C}_\vec{a}\vec{x}. \] すなわち、 \begin{align*} \vec{r}'&=\vec{r}-(\sin\phi)\,\vec{d}\times\vec{r}+(1-\cos\phi)\vec{d}\times(\vec{d}\times\vec{r})\\ &=\vec{r}-(\sin\phi)\,\hat{C}_\vec{d}\vec{r}+(1-\cos\phi)\,{\hat{C}_\vec{d}}^2\vec{r}\\ &=\left\{\hat{E}-(\sin\phi)\,\hat{C}_\vec{d}+(1-\cos\phi)\,{\hat{C}_\vec{d}}^2\right\}\vec{r}.\tag{8} \end{align*} ここで、$\hat{E}$は単位行列である。
北緯$\theta$の観測地における恒星の日周運動について考察してみる。まず、土台となる座標系を定義しておこう。天体観測では、しばしば地平座標系で天体の位置を指定する。この座標系は、観測者が原点にあり、高度角$h\in [-\pi/2,\pi/2]$と方位角$A\in[0,2\pi)$の二つがパラメータである。$h=\pi/2$は天頂であり、$h=0$が地平面である。また、方位角$A$は真北を$0$とし、時計回りを正と定義する。ここで、天体観測で星の向きを指定する分には、動径距離は重要でないことに注意する(数学的には射影空間を考えるということであり、天文学的には天球面を考えるということである)。よって、動径距離を1とした球座標系として地平座標系を再定義しても問題なく、ここでもそのようにして、星の向きを「天球面上の位置」として記述することにする。さらに、地平座標系に対応した直交座標系も定義しておこう。この座標系は、地平座標と原点を共有し、$x,y,z$軸の正方向をそれぞれ、東向き、北向き、天頂方向にとるものとする。
恒星が時刻$t_0$(単位は時)に高度角$h_0$、方位角$A_0$にあるとする。この恒星の位置は、直交座標系で \[\vec{r}=\begin{pmatrix}\cos h_0\sin A_0\\\cos h_0\cos A_0\\\sin h_0\end{pmatrix}\] と書くことができる。日周運動により、この恒星が時刻$t$に高度角$h$、方位角$A$へと動いたとき、これを記述することが目的である。まず、日周運動の回転極を表すベクトル$\vec{d}$と回転角$\phi$を調べよう。日周運動の回転極は天の北極である。天の北極は真北の方向、北緯に等しい高度角のところにあるため、直交座標系で、 \[\vec{d}=\begin{pmatrix}0\\\cos\theta\\\sin\theta\end{pmatrix}\] と決定できる。これは単位ベクトルであり、対応する外積行列は、 \[\hat{C}_\vec{d}=\begin{pmatrix}0&-\sin\theta&\cos\theta\\\sin\theta&0&0\\-\cos\theta&0&0\end{pmatrix}\] である。一方、回転角のほうは、日周運動が1時間で$15^\circ =\pi/12$だけ天の北極の周りを反時計回りに回ることを思い出せば、すぐに求められる: \[\phi=\frac{\pi}{12}(t-t_0).\] 以上の情報を用いれば、Rodriguesの公式を用いて日周運動が表現できる。
具体的な例として、南中1時間後のアンタレス (赤緯-26.4度) の、札幌 (北緯43.0度) における高度角と方位角を求める。回転軸ベクトル$\vec{d}$は、札幌の緯度から、 \[\vec{d}=\begin{pmatrix}0\\\cos 43^\circ\\\sin 43^\circ\end{pmatrix}\sim\begin{pmatrix}0\\0.7314\\0.6820\end{pmatrix}\] である。対応する外積行列とその二乗は、 \begin{gather*} &\hat{C}_\vec{d}= \begin{pmatrix} 0&-\sin 43^\circ&\cos 43^\circ\\ \sin 43^\circ&0&0\\ -\cos 43^\circ&0&0 \end{pmatrix} = \begin{pmatrix} 0&-0.6820&0.7314\\ 0.6820&0&0\\ -0.7314&0&0 \end{pmatrix},\\ &{\hat{C}_\vec{d}}^2= \begin{pmatrix} -1&0&0\\ 0&-\sin^2 43^\circ&\cos 43^\circ\sin 43^\circ\\ 0&\cos 43^\circ\sin 43^\circ&-\cos^2 43^\circ\\ \end{pmatrix} = \begin{pmatrix} -1&0&0\\ 0&-0.4651&0.4988\\ 0&0.4988&-0.5349 \end{pmatrix}. \end{gather*} また、1時間分の日周運動なので、回転角は$15^\circ$となる。
アンタレスの位置を求めよう。初期位置では南中していることから、アンタレスの初期方位は真南 ($A=180^\circ$) である。また、南中していることとアンタレスの赤緯・札幌の緯度から、アンタレスの初期高度角$h$は$90^\circ-43.0^\circ-26.4^\circ=20.4^\circ$と求められる。よって、直交座標系における初期位置$\vec{r}$は、 \[\vec{r}=\begin{pmatrix}0\\-\cos 20.4^\circ\\\sin 20.4^\circ\end{pmatrix}=\begin{pmatrix}0\\-0.9373\\0.3486\end{pmatrix}.\] 日周運動後の直交座標系での位置$\vec{r}'$を求めると、 \begin{align*} \vec{r}'=\left\{\hat{E} -(\sin 15^\circ) \begin{pmatrix} 0&-\sin 43^\circ&\cos 43^\circ\\ \sin 43^\circ&0&0\\ -\cos 43^\circ&0&0 \end{pmatrix} +(1-\cos 15^\circ) \begin{pmatrix} -1&0&0\\ 0&-\sin^2 43^\circ&\cos 43^\circ\sin 43^\circ\\ 0&\cos 43^\circ\sin 43^\circ&-\cos^2 43^\circ\\ \end{pmatrix} \right\} \begin{pmatrix}0\\-\cos 20.4^\circ\\\sin 20.4^\circ\end{pmatrix} \sim \begin{pmatrix}-0.2314\\-0.9165\\0.3263\end{pmatrix} \end{align*} となる。この$z$成分は高度角の正弦なので、日周運動後の高度角と方位角はそれぞれ、 \begin{align*} &h\sim\mathrm{Sin}^{-1}(0.3263)=19.04^\circ,\\ &A\sim \mathrm{Cos}^{-1}\left(\frac{-0.9165}{\cos h}\right)=194.2^\circ \end{align*} と求められる。
| もどる | next() |
Last Update: 2020/08/19
Copyright (C) Matsuoka Ryo All Rights Reserved.